Réseaux de Petri
Définition
Un réseau de Petri (aussi connu comme un réseau de Place / Transition) est un modèle mathématique servant à représenter divers systèmes (informatiques, industriels…)
Une place ne peut aller vers une autre place
Une transition ne peut aller vers une autre transition
Une place peut contenir des jetons
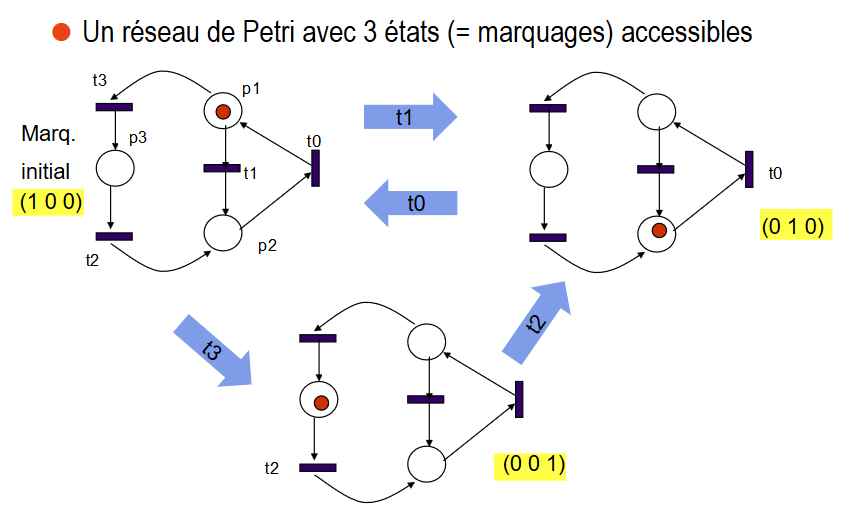
La répartition initiale des jetons sur les place du réseau s'appelle un marquage initial
Les places situées avant une transition (ici P1 et P2) sont des places d'entrée de cette transition
Les places situées après une transition (ici P3) sont des places de sortie de cette transition
La valuation d'un arc indique le nombre de jetons à consommer ou à produire lors du passage, du franchissement d'une transition
La valuation d'un arc reliant une place d'entrée à une transition est par défaut égale à 1. Elle sert à définir le nombre de jetons qui seront consommés par le franchissement de la transition
la valuation d'un arc reliant une transition à une place de sortie est par défaut égale à 1. Elle sert à définir le nombre de jetons qui seront produits par le déclenchement, le franchissement de la transition
Le nombre total de jetons n'est pas obligatoirement conservé, il peut augmenter ou augmenter
Définition d'une transition franchissable d'un réseau de Petri
Une transition est dire franchissable si et seulement si pour chaque place d'entrée, le nombre de jetons est supérieur ou égal à sa valuation en entrée de cette transition
La transition t1 dans l'exemple suivant est franchissable
Dans l'exemple ci dessus, on essaie de produire des vélos (place 3) à partir d'un cadre de vélo (place 1) et de 2 roues (place 2)
Combien de fois la transition t1 est-elle franchissable ?
Combien de fois la transition t1 est-elle franchie ?
Combien de vélos peut-on produire ?
Autre exemple
Ici on va désosser un vélo pour produire un cadre et deux roues
Graphe d'état d'un automate fini
Un automate fini ou automate avec un nombre fini d'états est un modèle mathématique de calcul..
Lorsqu'on a un graphe d'état, un jeton circule et la place occupée est celle correspondant à l'état en cours
Rouge
Exclusion mutuelle dans un réseau de Petri
Il y a exclusion mutuelle lorsqu'une place, en entrée d'un ensemble de transitions, ne possède pas assez de jetons pour permettre le franchissement de toutes ces transitions. Autrement dit lorsque le nombre de jetons est strictement inférieur à la somme des valuations.
Exemple de gestion de deux feux tricolores qui ne peuvent être verts en même temps
Le jeton dans la place P7 est requis pour qu'un feu tricolore passe au VERT
Il est rendu quand ce même feu tricolore repasse au ROUGE
La place P7 est utilisée pour permettre l'allocation de ressources
Rouge et Rouge
Autre exemple de réseau de Petri pour simuler un automate à 3 états
Parallèlisme
Synchronisation
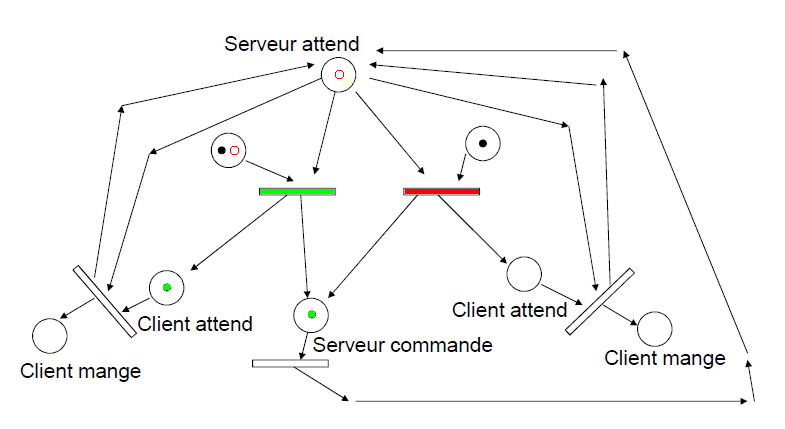
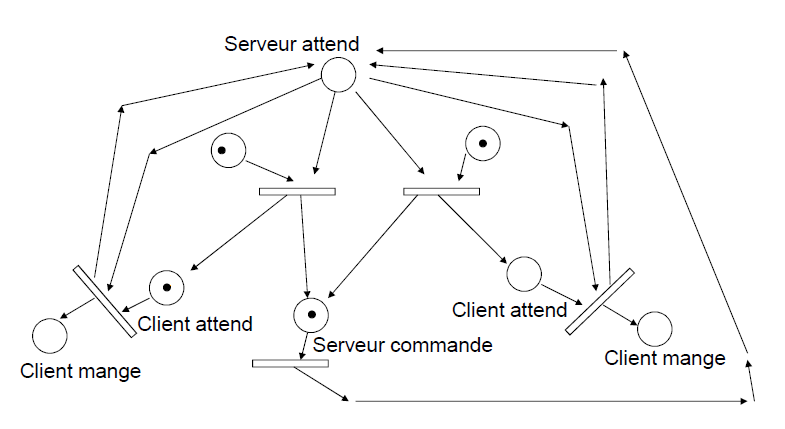
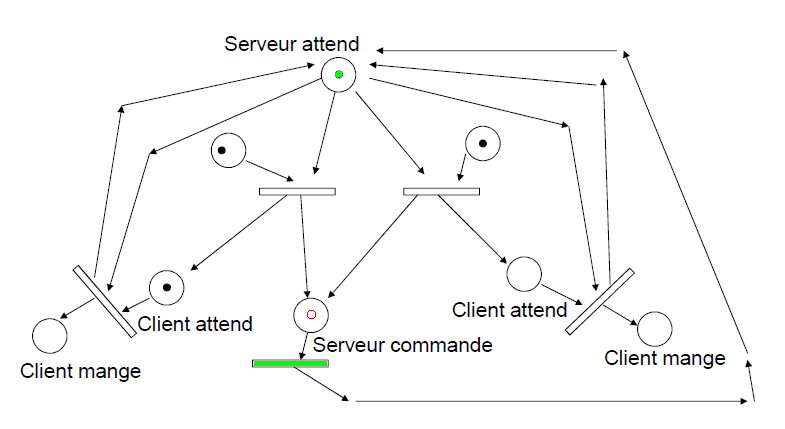
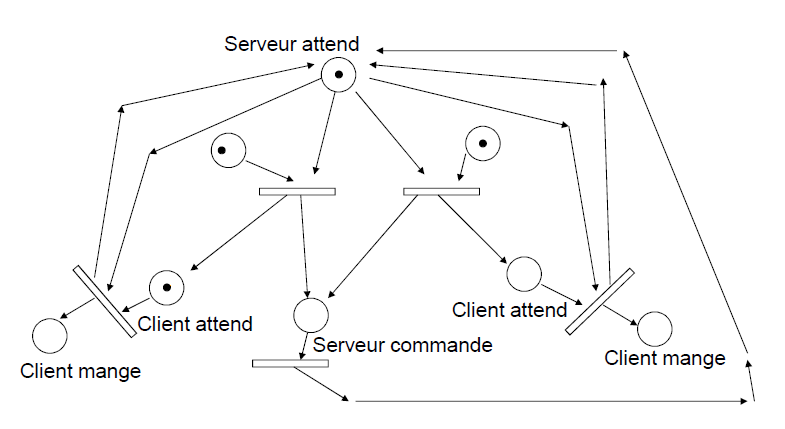
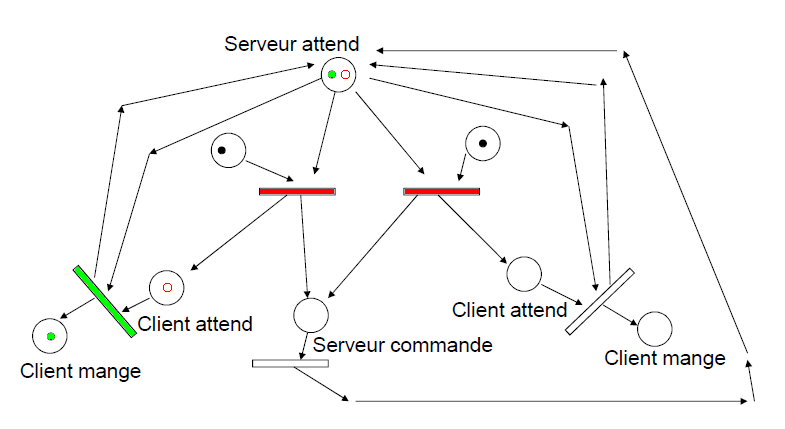
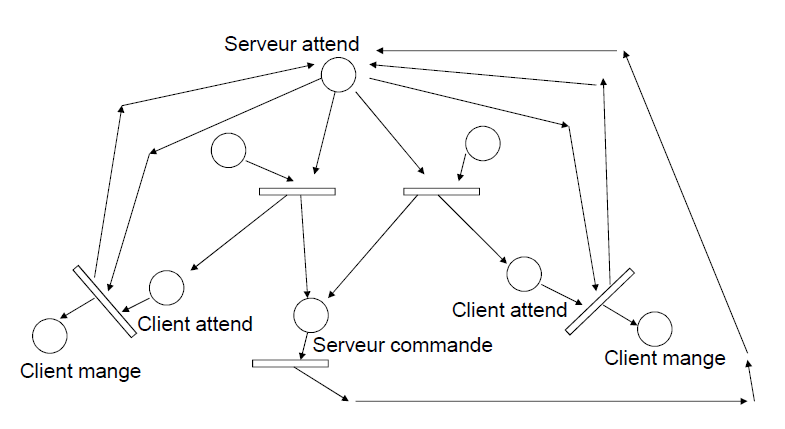
Simulation d'un service dans un restaurant
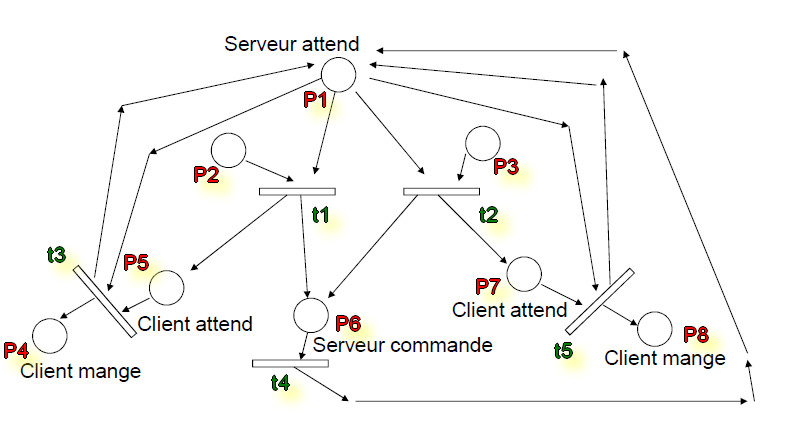
On veut simuler ici un restaurant avec deux files d'attente et un seul serveur
Marquage initial avec le serveur qui attend et 3 clients dont 2 à gauche et 1 à droite
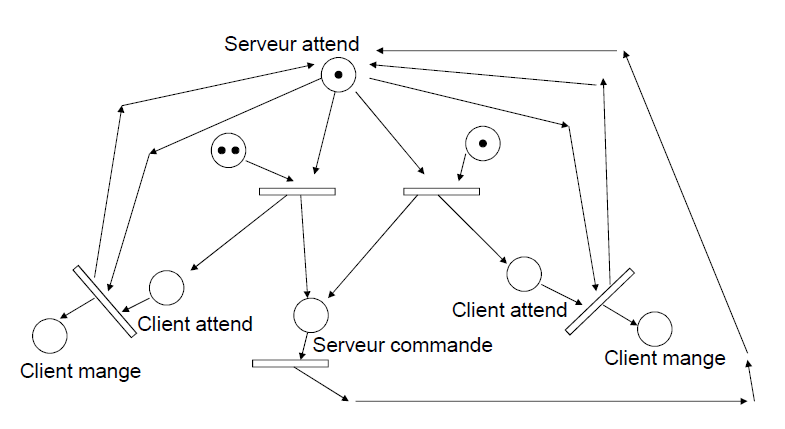
Les jetons des places d'entrée seront consommés en respectant la valuation (1 par défaut)
Les jetons des places de sortie seront produits en respectant la valuation (1 par défaut)
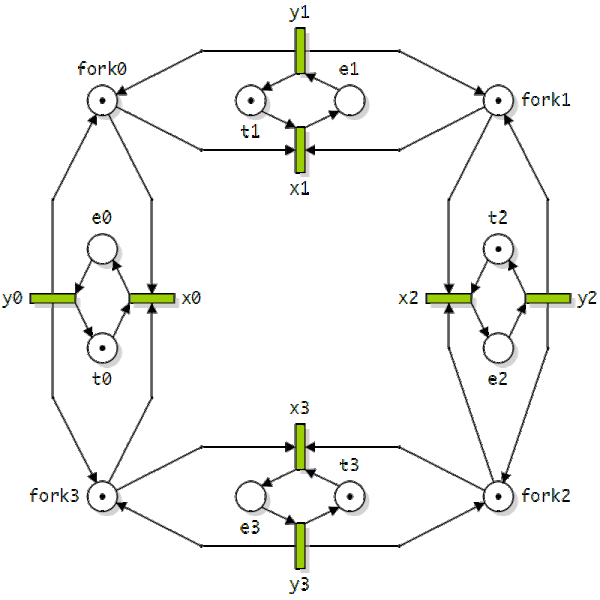
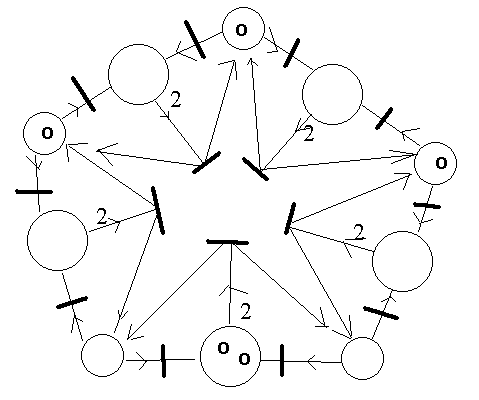
Les cinq philosophes
Quelles sont les transitions franchissables ?
Quelles sont les transitions en exclusion mutuelle ?
Faire évoluer ce réseau de Petri sur 3 itérations
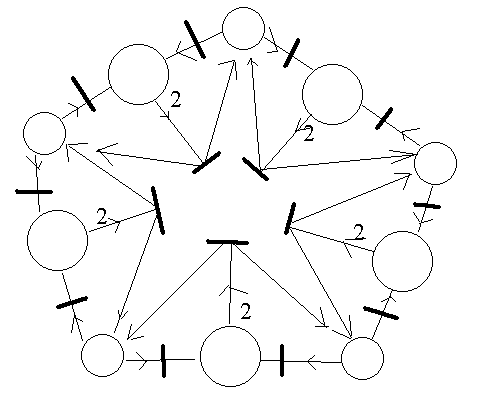
Refaire l'exercice avec le réseau de Petri donné dans les pages suivantes